Сравнение методов аппроксимации данных путём минимизации функций невязки различных видов

Актуальность

В современном мире статистика и анализ данных играют значительную роль. Потребность математически описать набор данных любой природы – от экспериментально полученных измерений при проведении школьной лабораторной работы по физике до задач синтеза речи, машинного обучения, нейронных сетей и искусственного интеллекта, обработки фото- и видеоматериалов, предугадывания компьютером возможного поведения человека –такая потребность универсальна и может возникнуть в различных областях исследовательской деятельности. Этими вопросами занимается регрессионный анализ – раздел математики, содержащий и изучающий набор статистических методов, позволяющих исследовать зависимость одной переменной от другой.

Цель

Сравнение различных методов аппроксимации (упрощения) данных

Задачи

1. Вывод формул

2. Изучение различных методов аппроксимации данных

3. Выбор языка программирования

4. Написание программы с дружелюбным к пользователю интерфейсом и наглядная визуализация различных методов

Оснащение и оборудование, использованное при создании работы

• Компьютер
• Система программных средств для разработки программного обеспечения

Описание

В ходе работы над теоретической частью проекта был изучен метод наименьших квадратов, самостоятельно выведены формулы для коэффициентов аппроксимирующих функций в различных случаях.

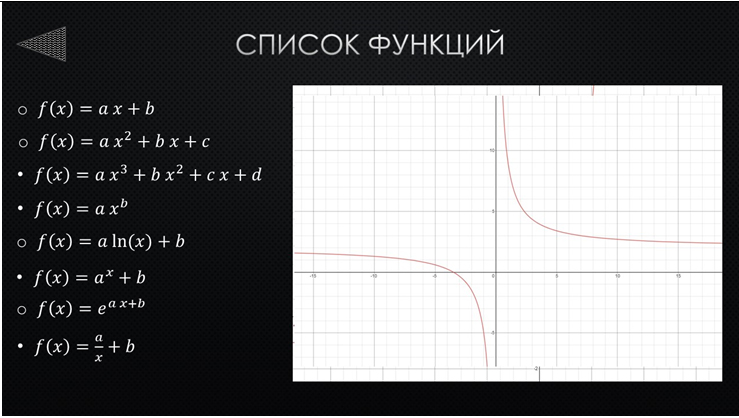
По литературным источникам был изучен и реализован эффективный алгоритм аппроксимации функций путём минимизации суммы модулей отклонений.

Создано программное приложение, позволяющее получить нужную аппроксимирующую функцию (одного или двух переменных) в виде формулы, построить её график (линию или поверхность), визуально оценить качество аппроксимации.

Результаты работы/выводы

Метод наименьших модулей имеет максимум функции правдоподобия, если ошибки измерения подчиняются закону Лапласа, в то время как метод наименьших квадратов – если ошибки распределены по Гауссу.

Визуальное сравнение результатов работы методов наименьших квадратов и наименьших модулей позволяет предположить, что в большинстве случаев кривая, построенная методом наименьших модулей, точнее описывает видимое расположение точек, «игнорируя» те из них, которые зрительно воспринимаются как случайное отклонение от общей тенденции.

Перспективы использования результатов работы

Результаты можно внедрять в учебный процесс для освещения альтернатив известных и изученных методов описания данных.